Konec éteru znamenalo ztrátu pevné vztažné soustavy (pevného bodu) ve vesmíru, a tím také zpochybnění univerzální platnosti Newtonovy mechaniky. Věhlasný fyzici (H. A. Lorentz, G. F. Fitzgerald, J. Larmor) navrhovali dílčí vysvětlení „záporného výsledku“ M-M experimentu v rámci Newtonovy mechaniky třírozměrného prostoru, kde čas. je invariantní entita – nezávislá na souřadnicovém systému v kterém se děje popisují.

K vysvětlení záporného výsledku M-M experimentu navrhl Einstein v roce 1905 radikálně novou Speciální teorii relativity (STR), která nepotřebuje pevný bod ve vesmíru (éter). STR je postavena na dvou postulátech:

• Postulát A Mechanické a elektromagnetické děje probíhají stejně ve šech inerciálních soustavách (pohybujících se rovnoměrně přímočaře bez rotace). Jinými slovy, všechny fyzikální zákony lze vyjádřit stejnými rovnicemi.
• Postulát B Rychlost světla je ve všech inerciálních soustavách stejná – invariantní.

Z postulátu B lze odvodit dilataci času (zpomalení plynutí času) a kontrakci délek (krácení délek ve směru rychlosti soustavy). Z postulátu A, s ohledem na dilataci času, kontrakci délek a Newtonova zákona síly, vyplývá relativistická hmotnost

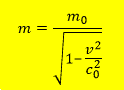
kde c₀ je rychlost světla v gravitace prostém vakuu, v – rychlost tělesa vzhledem ke klidové soustavě, a m₀ je hmotnost tělesa v klidu – je to tzv. atomární hmotnost tělesa, která vystupuje také v Newtonových zákonech. Na rozdíl od hmotnosti m v zákoně síly Newtonovy mechaniky, relativistická hmotnost je funkce rychlosti tělesa.Rychlost c₀ jsme označili dolním indexem 0, abychom zdůraznili, že se jedná o rychlost světla v gravitace prostém vakuu, jenž předpokládá speciální teorie relativity, a také Maxwellova teorie světla.

Stěžejní články [1], [2] Einstein napsal v roce 1905. V prvním z nich je uvedena speciální teorie relativity. Druhý článek vyšel o tři měsíce později a osahuje odvození slavné Einstejnovy rovnice E = mc₀², která vyjadřuje ekvivalenci hmotnosti a energie.

Uvedeme odvození rovnici ekvivalence hmotnosti a energie podle [4], abychom ji zbavili její „tajuplnosti“ a pronikli do významu její pravé strany. Vyjdeme ze vztahu pro kinetickou energii tělesa s klidovou hmotností m₀, které se dalo do pohybu vlivem působení síly F. Těleso se nachází v pohybu, proto musíme počítat s jeho relativistickou hmotností m a jeho hybností mv v Newtonovým zákoně síly.

Poslední rovnice je Einsteinova rovnice E=E₀+E_k=mc₀². Celková energie E je součet kinetické energie E_k a klidové energie E₀ =m₀c₀².

Jednotlivé veličiny v Einsteinovy rovnici E = mc₀² nyní formulujeme v hovorové řeči:

• E – je celková energie tělesa v dané konkrétní situaci (rychlost, teplota – horká voda má víc energie než studená).
• c₀² – je převodní koeficient mezi energii a hmotnosti, podobně jako je finanční kurz převodem mezi korunou a dolarem. Stojí za zmínku, že c₀ je rychlost světla v gravitace prostém vakuu, jejíž velikost je dána zafixováním číselné hodnoty 299 792 458 [m s^–1] přesně. Zafixovaná je také tím, že je uvedena v Zákoně o metrologii č. 505 z roku 1983 [7].
• m – součet jaderné hmotnosti m₀ a „přídavní hmotnosti“, která vznikne z „přídavné energie“ (kinetické, tepelné) přepočítané koeficientem c₀². Poznámka: Mluvili jsme již o gravitační hmotnosti, pak o relativistické hmotnosti, a v souvislosti s rovnici E = mc₀² můžeme mluvit o energii ekvivalentní hmotnosti.

Vzorec E = mc₀² je zákon ekvivalence, který přiblížíme ještě příkladem z říše Sci-Fi.
Představme si atomovou bombu o hmotnosti m₀ , která nám leží v pokoji na podlaze. Výše uvedenýma matematickými úpravami jsme dospěly k závěru, že její klidová energie je E₀ = m₀c₀², aniž bychom využili poznatek, že naše atomová bomba sestává z atomů. Ve skutečnosti klidová energie E₀ je jaderná energie. Při výbuchu bomby na podlaze se tato energie uvolní a projeví se to katastrofou (záření, destrukce, atd.).

Položme nyní naši atomovou bombu na stůl, kde leží v klidu. Její klidová energie je nadále E₀ = m₀c₀², ale navíc získala i gravitační potenciál ΔW_p= h*m*, kde m* je váha (síla) bomby o hmotnosti m₀, a h* je výška stolu nad podlahou. Při pádu bomby ze stolu, gravitační potenciál se postupně mění na kinetickou energii, a pokud máme štěstí, a bomba nevybuchne, její pád na podlahu nadělá škodu jen ve výši odpovídající okamžité kinetické energii E_k = ΔW_p = h*m*. Během pádu a dopadu bomby je její hmotnost stále m₀.

Pokud bomba spadne ze stolu na podlahu a přitom exploduje, pak způsobí katastrofu odpovídající součtu kinetické a klidové energie bomby – tj. celkové energii:

E = E_k + E₀ = h*m* + m₀c₀² = (h*m*c₀^–2 + m₀) c₀² = mc₀².
Kinetická energie (gravitační potenciál) přispívá k celkové hmotnosti m měrou h*m*c₀^–2.
Konec příkladu z říše Sci-Fi.

Einsteinovou rovnici E = mc² lze odvodit pomocí STR bez ohledu na existenci Newtonova gravitačního zákona a tudíž bez ohledu na gravitační pole, které může existovat i ve vakuu. Postulát STR o invariantnosti rychlosti světla vyslovil Einstein ve snaze se vyrovnat se ztrátou éteru jakožto nehybném prostoru, jak se o tom zmiňujeme výše v souvislosti s M-M experimentem. „Speciální teorii nikterak nenáleží neomezený obor platnosti; její výsledky platí jen potud, pokud nemusíme přihlížet k vlivům gravitačního pole na jevy (např. na světlo)“ ([3] str. 136). Einsteinova Obecná teorie relativity (OTR) z roku 1916 počítá i s vlivem gravitačního pole.